Com’è noto i metodi complementari non sono ritenuti, dalla normativa vigente, sostitutivi delle prove di accettazione, tipo A e tipo B, che devono essere effettuate in laboratorio su provini cubici formati con calcestruzzo prelevato dalla Direzione Lavori al momento del getto nelle casseforme. Tuttavia la normativa EN 13791:2006, Assessment of in-situ compressive strength in structures and precast concrete elements, chiarisce come e quando sia necessario determinare la resistenza a compressione del calcestruzzo in opera di una struttura:
• quando una struttura già esistente deve essere modificata o riprogettata;
• quando sorgono incertezze dovute a cause legate a negligenze di posa, di degrado del calcestruzzo causato da diversi fattori;
• quando sia necessaria la determinazione di tale resistenza durante le fasi costruttive del processo edilizio;
• quando vi sono delle difformità connesse con la resistenza a compressione ottenute dallo schiacciamento dei provini standard;
• quando tale determinazione viene richiesta in conformità ad una specifica di progetto;

I metodi complementari semplici, presi singolarmente, non forniscono molto spesso risultati accettabili; questa considerazione vale in particolar modo per lo sclerometro, per l’apparecchio ad ultrasuoni, per la pistola Windsor, per il “Pull-Out” ecc. Risultano più attendibili, invece, i metodi combinati, come il “Sonreb”, che, correlando due entità fisiche oggetto di indagine, consentono una determinazione più precisa; in realtà, anche il metodo appena citato non è sempre applicabile, dal momento che è necessaria la conoscenza di molti parametri che sono sconosciuti quasi sempre all’operatore incaricato della indagine.

Da qui la necessità di ricercare un metodo combinato, che possa essere applicato anche da chi non conosce la storia della struttura in esame, che sia di facile applicabilità e che richieda l’impiego di strumentazioni semplici, ma che, tuttavia, possa fornire dati e risultati statisticamente attendibili.

Ebbene, chi scrive, ha ideato e verificato sperimentalmente un metodo che è stato battezzato “γ-i”, volendo con ciò evidenziare che ci si avvale dell’impiego di uno sclerometro, la lettera “i” sta per indice di rimbalzo, e del valore della massa volumica del calcestruzzo in opera indicata con la lettera “γ”.

Con il metodo che si propone, lo sclerometro viene utilizzato in modo anomalo rispetto alle indicazioni del costruttore, che mirano ad illustrare le corrette modalità di impiego dello stesso strumento; qui infatti si impiega lo sclerometro come martello compattatore dello strato superficiale della struttura e non come indagatore della durezza superficiale.

Tale metodo, quindi, che è stato ampiamente illustrato negli articoli citati in testa, correla due grandezze fisiche basilari del calcestruzzo in opera:
- la compattabilità superficiale;
- la sua massa volumica;
ponendosi come obiettivo la determinazione del valore Rc (resistenza cubica) del calcestruzzo in opera.

Lo sclerometro, dunque, non viene impiegato per indagare sulla durezza superficiale del calcestruzzo, obiettivo per cui è stato ideato, ma sulla sua capacità di compattarsi superficialmente a seguito di urti ripetuti e provocati in aree ristrette dalla punta dell’apparecchio.
Le battute sono effettuate su punti prestabiliti e vengono ripetute tre volte per ogni punto senza spostare mai lo strumento durante l’effettuazione delle tre battute; si ottengono, per ogni punto, valori crescenti dell’indice di rimbalzo ed in particolare mediamente si nota un incremento del 20% tra la seconda e la prima battuta e del 10% tra la terza e la seconda battuta.

Si è riscontrato sperimentalmente che un numero di battute maggiore alle tre, previste dal metodo, nell’85% circa dei casi non fa aumentare l’indice di rimbalzo e nel rimanente 15% non si verificano aumenti significativi.

Lo studio del metodo può considerarsi ormai ultimato, dopo ripetute verifiche che hanno interessato anche calcestruzzi di elevata resistenza, strutture ad armatura lenta, prefabbricate e precompresse; da qui la decisione, dopo una ulteriore valutazione in termini statistici, di farne oggetto di pubblicazione su riviste specialistiche del settore.

Una osservazione che ritengo degna di essere menzionata riguarda il fatto che si è sperimentalmente riscontrata la migliore applicabilità del metodo ai manufatti in calcestruzzo molto stagionati, si è cioè constatato che più i manufatti sono antichi e più precisa è la stima della resistenza meccanica; ciò risolve uno dei maggiori inconvenienti all’applicabilità del metodo sclerometrico tradizionale per il quale infatti la carbonatazione del calcestruzzo stagionato costituisce un grosso problema in merito all’attendibilità dei risultati ottenuti.

Per una migliore comprensione del metodo si riporta di seguito una breve descrizione delle fasi operative, con l’ausilio di un esempio numerico.


B - FASI OPERATIVE DE METODO “γ-i”

1) Supponiamo di dover indagare una struttura in calcestruzzo semplice. Sul manufatto si scelgono n° 3 fasce (alta, mediana, bassa), ritenute significative, su cui effettuare le indagini, ed all’interno di ognuna di queste si individua una zona (X, Y, Z) su cui effettuare le battute (Fig. 1);

2) all’interno di ognuna di queste zone si individuano n° 12 punti disposti su tre file, (Fig. 2);

3) su ogni punto si effettuano n° 3 battute con lo sclerometro avendo cura di non disallineare la punta durante le tre letture e mantenendola sempre a contatto con la superficie su cui si interviene. I valori letti si riportano su apposite tabelle (Fig. 3).

A titolo d’esempio, si riportano nelle Tabelle 1, 2 e 3 gli indici di rimbalzo riscontrati in una ipotetica indagine; nell’esempio ci si limita a valori letti su una faccia della struttura, nella realtà è opportuno ripetere le operazioni anche sulla faccia opposta (laddove è possibile) in corrispondenza delle zone X,Y,Z per effettuare poi la media dei valori ottenuti.

Nelle tre tabelle sono evidenziati per ogni serie di battute i valori rispettivamente minore (colore verde) e maggiore (colore rosso) che vengono scartati.

Il metodo prende in considerazione le tre battute sclerometriche su ogni punto individuato, al fine di indagare sulla compattabilità iniziale, media e finale del calcestruzzo, e la sua massa volumica; i due parametri fisici sono messi in relazione attraverso la seguente espressione, essendo 90 il numero delle battute effettuate:

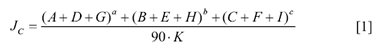
dove:
• J_c è l’indice di rimbalzo corretto;
• 90 è il numero delle battute effettuate;
• K è un coefficiente che assume il valore 1 per i calcestruzzi semplici e 0,95 per quelli armati.

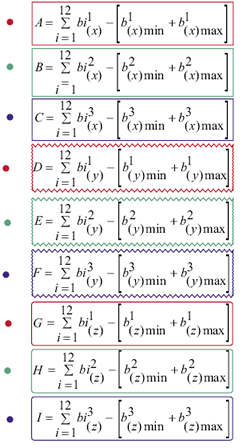
Il pedice indica la zona interessata (zona x = riquadro semplice, zona y = riquadro zigzagato, zona z = riquadro zebrato) e l’apice indica la battuta (1= prima battuta : punto rosso, 2 = seconda battuta: punto verde, 3 = terza battuta: punto azzurro)

Gli esponenti a, b, c, dell’equazione, si possono leggere sull’abaco di Fig. 4, costruito riportando su un sistema di assi cartesiani i valori ottenuti dalle numerose sperimentazioni effettuate. È, comunque, consigliabile non ricorrere all’abaco per leggere i dati ma ottenerli analiticamente mediante le seguenti espressioni costruite sfruttando il parallelismo delle tre rette inclinate contenenti i tre fattori esponenziali.

Come si può notare, nelle suddette equazioni interviene il valore di “γ”, massa volumica del calcestruzzo, che necessariamente dovrà essere determinato mediante prelievi da effettuare sulla struttura oggetto dell’indagine.

C - ELABORAZIONI

Riferendosi all’esempio numerico sopra riportato, si utilizza il valore della massa volumica del calcestruzzo, con cui è realizzato il manufatto, ricavato dal prelievo di almeno n° 3 carote.
Supponiamo che il valore medio della massa volumica sia pari a 2.330 Kg/m³; seguendo il metodo grafico dovremmo ricercare sull’asse delle ascisse di Fig. 4 il valore di 2.330, poi intercettare le rette (a,b,c) riportate nell’abaco con la verticale passante per quel valore di γ quindi rintracciare sull’asse delle ordinate i valori esponenziali, rispettivamente a – b – c.

Nel caso in questione l’abaco non consente questa operazione poiché non è stato aggiornato con l’introduzione dei nuovi risultati provenienti da ulteriori prove sperimentali che ne avrebbero allargato l’applicabilità e questo perché, come detto precedentemente, è consigliabile (metodo analitico) l’impiego delle equazioni 2) per ricavare i valori degli indici esponenziali, con maggiore precisione.

Nel caso specifico, dal calcolo si ottengono i seguenti valori:

a = 0,98687; b = 0,94818; c = 0,94014

Di seguito sono riportati i valori medi delle battute sclerometriche con i relativi totali:

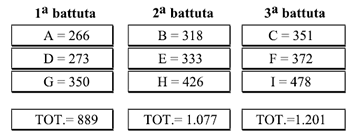
Sostituendo nell’equazione 1) i dati ottenuti si determina il valore corretto dell’indice di rimbalzo:

Ottenuto l’indice di rimbalzo corretto, dalla Tabella 4*** di conversione degli indici di rimbalzo in resistenze meccaniche, si ricava:

R_c = 18,0 N/mm²

Se ci fossimo fidati dei soli valori dell’indice di rimbalzo di prima battuta, così come si procede utilizzando lo sclerometro in modo canonico, avremmo ottenuto:

889/30 = 29,63 da cui: R_c = 23,5 N/mm²

Commettendo un errore in eccesso di circa il 24%.

D - CONCLUSIONI
Il metodo complementare combinato γ-i, descritto in questo articolo, permette di rilevare, mediante la procedura sopra riportata, un valore della resistenza cubica del calcestruzzo in opera, oggetto dell’esame, più aderente alla realtà di quanto non si ottenga impiegando lo sclerometro in forma canonica, e ciò continuando ad impiegare lo stesso apparecchio, anche se in modo difforme, che è molto semplice da usare, di facile trasportabilità e non distruttivo. Tuttavia il metodo richiede un prelievo per poter determinare la massa volumica del calcestruzzo in opera, ma ciò può essere effettuato mediante l’estrazione di micro carote che non possono quindi essere considerate il prodotto di un metodo distruttivo. Tale metodo, inoltre, può rappresentare una valida indagine preliminare prima di procedere, eventualmente, a metodi più sofisticati e complessi, anche in termini economici.

E - BIBLIOGRAFIA ESSENZIALE

1. Salvatore Lo Presti, Antonio Cerami, Prove Sperimentali Non Distruttive per la Determinazione della Resistenza Caratteristica Cubica dei Calcestruzzi Cementizi, in L’Industria delle Costruzioni n. 225/6, Roma, luglio-agosto 1990.
2. Salvatore Lo Presti, Metodo Complementare Non Distruttivo per la Determinazione del Valore Caratteristico Rck dei Calcestruzzi in Opera. – Note Esplicative, allegato agli atti del convegno: Tecniche non Distruttive di Indagini Sperimentali su Stutture, Palermo, marzo 1995.
3. EN 13791, Assessment of in-situ compressive strength in structures and precast concrete components;
4. UNI EN 12504 (parti 1,2,3,4), Prove sul calcestruzzo nelle strutture, Carotaggi, Sclerometro, Prova ad ultrasuoni, Forza di estrazione;
5. V. Alunno Rossetti, Il Calcestruzzo, Materiali e Tecnologia, Ed. Mc Graw-Hill, 2003;
6. M. Collepardi, Il Nuovo Calcestruzzo, IV Edizione, Ed. Tintoretto, Villorba, 2006;
7. L. Coppola, Concretum, I Edizione, Ed. Mc Graw-Hill, 2007;
8. R. Marino, Autori Vari, La durabilità delle opere in calcestruzzo, Calcestruzzi SpA, Ed. La Fiaccola, 2007.