L’analisi della bibliografia sul tema della corrosione localizzata (nota come pitting corrosion nella letteratura internazionale), ha mostrato una elevata incertezza nella definizione dei parametri del modello di diffusione. Questo, dipende sostanzialmente dalla variabilità intrinseca di alcuni parametri, dall’insufficiente o inadeguata disponibilità di dati, ma anche dall’alto numero di semplificazioni che durante gli anni sono stati applicati al modello di penetrazione dei cloruri. Nel dettaglio, alcuni parametri geometrici e meccanici sono ben definiti perché sono disponibili un gran numero di dati sperimentali. Altri parametri invece non sono ben definiti a causa dei pochi dati sperimentali disponibili o perchè il modello fisico assunto è estrapolato empiricamente o è semplificato e perciò meno rappresentativo del processo reale.

Questo è particolarmente vero per esempio per il coefficiente di diffusione dei cloruri nel calcestruzzo o per il fattore d’età, descritto successivamente. Perciò, un altro punto preliminare importante di indagine del presente lavoro, concerne la scelta del miglior modello deterministico di penetrazione dei cloruri, al fine di stimare i parametri in maniera più rigorosa. Quindi, allo scopo di ricercare una predizione a lungo termine più accurata di diffusione dei cloruri nel calcestruzzo, è necessario includere la dipendenza dal tempo del tasso di diffusione nelle procedure di analisi e nella ricerca dei parametri di taratura.

Come dimostrato da diversi autori, come Mangat e Molloy [2] o Mejlbro [3], la soluzione standard della seconda legge di Fick è ottenuta partendo dall’assunzione che il coefficiente di diffusione sia costante nel tempo, quindi non è una procedura accurata ed è stato dimostrato che i suoi risultati applicativi sono troppo conservativi a causa della mancanza di considerazioni degli effetti ritardanti sul processo di diffusione risultante dal legame dei cloruri e dal raffinamento della struttura dei pori col passare del tempo [4]. A dispetto di questa assunzione semplificativa, questo modello è convenzionale ed è stato largamente usato dagli ingegneri nelle applicazioni pratiche, in virtù delle loro relativamente semplici espressioni matematiche. Anche se il confronto di questi modelli con la soluzione standard di Fick non mostra una differenza sostanziale di correlazione con i dati sperimentali, una differenza concettuale non trascurabile deve essere rilevata. Comunemente, infatti, gli effetti della dipendenza dal tempo sono stati presi in considerazione sostituendo semplicemente una relazione largamente diffusa, del coefficiente di diffusione in funzione del tempo D_a(t) con il coefficiente di diffusione che appare nella soluzione standard della seconda legge di Fick portando ad un errore analitico e concettuale.

Perciò, una relazione più accurata della legge di Fick deve incorporare la dipendenza del tempo del coefficiente diffusione e alcuni ricercatori hanno anche integrato la legge di diffusione tenendo conto della dipendenza dal tempo della concentrazione superficiale di cloruri [3]. Queste relazioni matematiche migliorate sono usate per predire più rigorosamente la concentrazione di cloruri con la profondità e il tempo. Due di questi modelli migliorati [2,3] sono stati scelti dagli autori per essere testati con dati sperimentali per mezzo di un algoritmo genetico (AG), al fine di ottenere parametri deterministici di calibratura del modello. Infine è stata ottenuta una valutazione deterministica più affidabile dei parametri del modello basata sulla procedura di taratura della dipendenza dal tempo.

1. MODELLI DI PENETRAZIONE DEI CLORURI

1.1 Modello convenzionale di penetrazione

Modelli differenti per la penetrazione dei cloruri sono stati elaborati e molte delle indagini sperimentali sono state condotte negli anni. Una procedura semplificata è basata sull’assunzione che il processo di diffusione dei cloruri può essere modellato per mezzo della seconda legge di Fick, come per la prima volta intuito da Collepardi et al. [5]. Avendo solo risultati disponibili da esperimenti di breve durata, e probabilmente anche a causa di difficoltà matematiche, essi considerarono solo il caso del coefficiente di diffusione costante e della concentrazione superficiale dei cloruri costante. Questa è una ipotesi diffusa (anche adottato da Stewart e Rosowsky [6]).

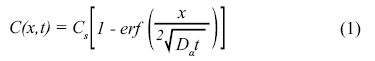
dove:
- C(x,t) è il contenuto di cloruri (in 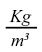) a una distanza x (in m) in un istante generico di tempo t (in s);
- C_s è la concentrazione superficiale di cloruri (in );
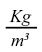- D_a è il coefficiente di diffusione apparente (in ).

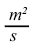Usando l’Eq. (1), è possibile definire il tempo d’innesco della corrosione con riferimento ad una assegnata concentrazione critica di cloruri sulle barre (definito come C_m).

Il coefficiente di diffusione dei cloruri D_a è assunto come valore costante anche se è dipendente dal tempo. Questa è una semplificazione evidente: infatti, il suo valore diminuirà col passare del tempo da quando il sistema di pori capillari sarà alterato durante la formazione dei prodotti di idratazione del cemento [2]. Takewake e Mastumoto [7] sono probabilmente i primi che stabilirono la dipendenza del coefficiente di diffusione dei cloruri D dal periodo di esposizione t ed usarono una equazione puramente empirica per descrivere la diminuzione del coefficiente di diffusione col tempo, che è proporzionale a t^−0.1. Più tardi, Tang e Nilsson [8] dai loro test di diffusività rapida trovarono che il coefficiente di diffusione misurato nel calcestruzzo giovane diminuiva drammaticamente con gli anni e proposero un’espressione matematica per un coefficiente di diffusione dei cloruri dipendente dal tempo basato sulla matematica della diffusione di Crank [14]. Test di laboratorio [10,2] e risultati su strutture esistenti [11] mostravano che la dipendenza del coefficiente di diffusione dall’età del calcestruzzo segue una linea retta in un sistema di coordinate logaritmiche.

Questo significa che il coefficiente di diffusione poteva essere scritto come una funzione potenziale [12]:

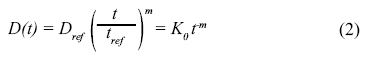
dove D(t) è il coefficiente di diffusione al tempo t; D_ref, il coefficiente di diffusione a un dato tempo di riferimento t<sub>ref e m è una costante che dipende dalle proporzioni della miscela. K0 incorpora tutte le costanti ed è definito come il coefficiente di diffusione effettivo al tempo t di riferimento.

Questa equazione tiene conto dell’influenza del tempo sulla diffusività.

Valori di m per calcestruzzi differenti devono essere ancora stabiliti, sebbene alcuni valori sono stati pubblicati [13–14]. Ulteriori ricerche utili ha quantificare questo parametro aiuterebbero a migliorare l’accuratezza di predizione della vita utile.

L’applicazione della Eq. (1) è molto comune in letteratura ed è anche presente in diverse linee guida sulla durabilità di opere in calcestruzzo, come ad esempio il documento sviluppato dal progetto EU DuraCrete (1998), [15]. Il modello DuraCrete è un modello empirico che utilizza la seconda legge di Fick come base teorica ed ha la seguente forma:</sub>

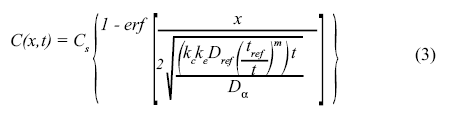
É chiaro che la presenza dei due fattori moltiplicativi k_c e k_e, due costanti introdotte al fine di considerare la natura probabilistica dell’aggressività dell’ambiente (k_e – costante ambientale) e le proprietà dei materiali (k_c – fattore di stagionatura), non cambia la caratteristica matematica del profilo di penetrazione già descritto. Infatti, il modello DuraCrete è stato sviluppato sulla base della semplificazione che il coefficiente di diffusione è costante nel tempo. Tuttavia, al fine di considerare anche gli effetti della dipendenza del tempo è stato suggerito di sostituire il valore di D_a che appare nella Eq. (1) con la relazione (2). Con questa semplificazione matematica, l’Eq. (3) sottostima fortemente il coefficiente di diffusione apparente e la sua applicazione ha determinato errori grossolani nei progetti di durabilità e recupero di strutture in calcestruzzo armato come sottolineato di diversi autori (si veda ad esempio [4]).

1.2 Modello di penetrazione con il coefficiente di diffusione dipendente dal tempo

Già nel 1980 ci si era resi conto che il modello semplificato standard, su cui si basava l’Eq. (1), dava un trasporto di cloruri non realistico, specialmente quando le predizioni a lungo termine erano basate su risultati dei test a breve termine [16]. Si dovrebbe notare che il coefficiente di diffusione apparente D_a nell’Eq. (1) è assolutamente diverso da D(t) dell’Eq. (2), in quanto D(t) è una funzione del tempo e come tale non può essere inserita direttamente nella soluzione della funzione errore (Eq. 3) senza essere integrata rispetto al tempo.

Risulta quindi che le predizioni del tempo di servizio erano spesso troppo brevi. La ragione di questo errore è l’assunzione del coefficiente di diffusione come costante, il quale conduce ad un’alta profondità di penetrazione non realistica. Per una predizione accurata della diffusione dei cloruri nel calcestruzzo, la dipendenza dal tempo del tasso di diffusione necessita di essere incorporato nella procedura di analisi, ricavando correttamente la seconda legge di Fick. Questo modello venne sviluppato da [2], portando all’equazione seguente:

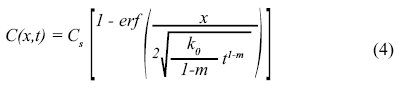
1.3 Modello di penetrazione con concentrazione superficiale dei cloruri dipendente dal tempo

Esistono altre soluzioni della seconda legge di Fick che considerano una concentrazione superficiale dei cloruri variabile. Alcuni ricercatori hanno infatti osservato che la concentrazione di cloruri sulla superficie esposta di strutture in ambiente marino era dipendente dal tempo. Sulla base delle osservazioni venne proposto di assumere che C_s aumentava con la radice quadrata del tempo [17]. Uji et al. ipotizzarono, anche basandosi sull’esame di costruzioni marine Giapponesi, che la concentrazione dei cloruri sulla superficie dipendeva dal tempo. Ciò rappresentava la scelta più opportuna da quando Crank [9] aveva pubblicato una soluzione della seconda legge di diffusione di Fick in condizioni di esposizioni all’ambiente marino. Dalle osservazioni fatte da Swamy et al. [18] si concluse che il modello migliore per rappresentare l’aumento di C_s con il tempo era una funzione potenziale. Mejlbro [3] propose che il modello di penetrazione dei cloruri dovrebbe essere descritto dalla seguente funzione:

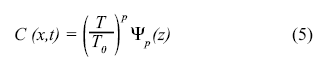
dove T è la variabile del tempo modificata:

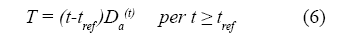
con D_a(t), che è l’equivalente di D(t) come definito nell’Eq. (2), e T₀ è introdotto al fine di ottenere un rapporto adimensionale. L’esponente p dipende da come C_s aumenta col tempo, cioè soprattutto dal tipo di legame e condizioni ambientali, mentre la funzione Ψp(z), dove z=x/√4T, soddisfa un’equazione differenziale ordinaria di secondo grado che può essere risolta per mezzo di una espansione in serie. I dettagli matematici sono disponibili su [3].

2. ANALISI DEL MODELLO MIGLIORE

Modellare l’ingresso dei cloruri è una base importante per progettare strutture di rinforzo in calcestruzzo e per stimare la vita delle strutture. Questi autori considerano molto importante superare alcune limitazioni concettuali e anche errori che possono capitare considerando modelli standard semplificati come quelli definiti nell’Eq. (1) e (3) o altre funzioni derivate usando procedure e assunzioni matematiche equivalenti. Infatti, anche se negli anni scorsi i modelli usati nell’Eq. (1) e (3) sono stati applicati nella progettazione di un gran numero di costruzioni strategiche, alcuni autori [4] hanno osservato che è necessario valutare gli errori compiuti nella stima del tempo di vita utile, dovuti a queste semplificazioni matematiche assunte nei modelli, e riprogettare con nuovi modelli più raffinati. Diversi autori infatti (per esempio, [19, 10]), sembrano aver semplicemente sostituito il coefficiente di diffusione costante nella soluzione della funzione errore della seconda legge di Fick con D dipendente dal tempo, senza chiarire adeguatamente le basi matematiche. L’errore matematico commesso, che consiste nel trascurare il termine t^1-m/(1-m) che appare nell’Eq. (4), ha come risultato una significativa differenza tra il coefficiente di diffusione K₀ che appare nell’Eq. (4) e lo stesso coefficiente D_a che appare nell’Eq. (3), come dimostrato da Luping et al.[4].

Sempre Luping et al. [4] affermano che i modelli semplificati potrebbero essere usati per predizioni a lungo termine senza errori matematici significativi se il fattore d’età m fosse più piccolo di 0.3; potrebbe sottostimare la vita di servizio se fossero utilizzati alti valori di m. Dal punto di vista della sicurezza strutturale, questa sottostima potrebbe essere accettabile perchè è conservativa, specialmente considerando il fatto che c’è ancora mancanza di informazione circa gli effetti a lungo termine del coefficiente di diffusione dipendente dal tempo [4]. Comunque, questo modello non potrebbe essere utilizzato per ottenere coefficienti di diffusione apparenti da esposizioni di breve termine, perchè in questo caso il modello sovrastimerà tremendamente il coefficiente di diffusione apparente. In altri approcci semplificati, diversi autori hanno provato a determinare un valore istantaneo del coefficiente di diffusione e non un unico valore che rappresentasse la media sull’intero periodo d’osservazione. Per esempio, Gulikers [20] presenta un nuovo fattore modificato della soluzione della funzione errore e Nilsson [21] presenta un simile coefficiente di diffusione istantaneo modificato. Un valore medio di D è usato invece da Stanish e Thomas [22] in cui il valore di diffusione è la media del coefficiente di diffusione variabile sul periodo di osservazione, il quale è calcolato dall’inizio fino al completamento del test di diffusione.

E’ chiaro pertanto che i risultati più importanti dello stato dell’arte sono divisi in due direzioni principali: il primo è basato su assunzioni e semplificazioni che dissociano fortemente il modello dal processo fisico, portando a risultati inaffidabili. Questo è quanto descritto in riferimento a diversi modelli nei quali la dipendenza dal tempo del coefficiente di diffusione D(t) non è stato considerato nella seconda legge di Fick e poi opportunamente risolta. La seconda direzione è seguita da un gruppo di ricercatori che hanno applicato più rigorosamente il modello di penetrazione dei cloruri il quale è ottenuto considerando correttamente la natura variabile nel tempo del coefficiente di diffusione.

Tuttavia, a dispetto di questo approccio più corretto, la stima dei parametri principali non considera la presunta variabilità col tempo. Infatti, in questi casi i valori istantanei del coefficiente di diffusione sono definiti per un dato istante di tempo ma non sono validi sull’intero periodo di tempo analizzato. Per la ragione descritta prima e per la grande variabilità mostrata con cui la legge di diffusione è stata risolta in letteratura, conducendo a valori differenti dei parametri principali del modello, nel presente articolo, il miglioramento della valutazione del tempo di servizio passa per la scelta del miglior modello di taratura al fine di individuare più accuratamente i parametri più importanti. Questa parte dell’analisi è importante al fine di considerare modelli più raffinati per rappresentare il processo fisico e determinare i parametri principali. A questo punto, perciò, si prova ad evitare alcune semplificazioni concettualmente errate nella definizione del modello, come le assunzioni più comuni della indipendenza dal tempo del coefficiente di diffusione.

2.1 Analisi di confronto tra la predizione e i profili misurati di cloruri basato sull’algoritmo genetico

L’analisi di taratura del modello è basato sui dati sperimentali di Thomas e Bamforth [14], riportati in Tabella 1, applicata a tre miscele di calcestruzzo: calcestruzzo con cemento Portland (CP), calcestruzzo con ceneri volanti (CV) e calcestruzzo con cemento di loppa d’altoforno (CLA). Anche se la procedura proposta dagli autori è usata per determinare il profilo dei cloruri, essa mostra una correlazione molto buona con i dati sperimentali, ma soffre di una limitazione concettuale significativa. Questo è dovuto al fatto che essi assumono inizialmente la soluzione standard come scritta nell’Eq. (1), trovando i valori di C_s e D_a come migliori parametri di taratura, tramite iterazione. Allo stesso tempo assumono la relazione (2) che descrive il coefficiente di diffusione in funzione del tempo, al fine di tenere in considerazione gli effetti della dipendenza dal tempo non considerati nel precedente modello. Da quest’ultima equazione, essi ottengono i valori di D₂₈ e m che meglio si adattano ai dati. Il miglior criterio di interpolazione usato era la somma del quadrato degli scarti tra la predizione del modello e i dati sperimentali [14]. Partendo da questi dati, allo scopo di determinare i parametri campioni da adottare nelle successive analisi di stima del tempo di vita utile, viene applicata nel presente lavoro una nuova procedura basata sull’algoritmo genetico. Gli autori hanno deciso di usare i dati di Thomas e Bamforth perchè questi dati sono estesi su un lungo periodo di tempo, ma è stato abbandonato l’approccio usato dagli autori menzionati a causa delle incoerenze procedurali emerse dalle loro analisi, come spiegato precedentemente. Nel seguito, adottando i due modelli dipendenti dal tempo dell’Eq. (4) e (5), perciò calibrandoli anche in funzione della variabile tempo, si cerca di migliorare matematicamente la stima dei parametri.

Lo scopo di questa sezione è usare i dati ottenuti da Thomas e Bamforth per fare un confronto tra il modello convenzionale e i due modelli evolutivi. I risultati ottenuti dagli autori citati sono assunti come riferimento per il primo modello menzionato (Eq. (1)). La necessità di introdurre questa procedura di calibrazione nasce dalla osservazione che il coefficiente di diffusione, come largamente studiato, è fortemente dipendente dal tempo di esposizione e perciò, al fine di considerare questa variabilità col tempo, è necessario che venga esaminato un modello che incorpori in maniera appropriata questo effetto. Per questa motivo, sono stati considerati i modelli su cui sono basate l’Eq. (4) e (5). Una volta assunti questi modelli “evolutivi”, il successivo miglioramento nella stima dei parametri consiste nel calibrarli come funzione del tempo. In questo modo, il profilo dei cloruri non è più definito in uno spazio bidimensionale che descrive la concentrazione dei cloruri con la profondità ad un tempo fissato, ma deve essere dipendente anche dal tempo. Perciò, la tecnica di rettifica è sviluppata in uno spazio tridimensionale di profondità e tempo. Solo in questa maniera, è possibile stimare rigorosamente il coefficiente di diffusione e tener conto della sua variazione col tempo. Infatti, come descritto in seguito, Thomas e Bamforth non ottengono un unico valore del coefficiente di diffusione, ma uno istantaneo, riferito ad uno specifico istante di tempo. Invece, usando la procedura di calibrazione che tiene conto della variazione del tempo sui modelli evolutivi definiti in precedenza (Eq. (4) e (5)), è possibile stimare un unico valore del parametro di diffusione. Al fine di conseguire questo scopo, la procedura sviluppata in questo lavoro è governata da un algoritmo genetico (AG) il quale è usato come strumento per minimizzare la somma dei quadrati degli scarti valutati come differenza tra la predizione del modello e i dati sperimentali. Tale metodo è applicato al fine di determinare il profilo dei cloruri e generare i valori di taratura dei parametri, prendendo simultaneamente in considerazione sia la variabile tempo che la profondità.

I risultati del confronto sono riportati di seguito. I profili dei cloruri misurati su tre tipi di calcestruzzo sono usati per testare la correlazione dei due modelli migliorati dipendenti dal tempo. Allo scopo di semplificare la notazione, il modello alla base dell’Eq. (4) sarà chiamato ‘Modello A’ e il profilo dell’Eq. (5) sarà chiamato ‘Modello B’. Per ognuno di questi modelli è tracciato il grafico del profilo dei cloruri che meglio si adatta ai dati sperimentali. A titolo d’esempio, i profili in funzione del tempo e della profondità sono riportati in Fig. 1.a (in alto) con riferimento al solo Modello A, nel caso del cemento Portland. Il grafico a curve di livello dello stesso profilo di penetrazione dei cloruri, con il valore numerico dei dati sperimentali (numero bianco) e quello di predizione del modello (numero nero) per le tre tipologie di miscele di calcestruzzo, è mostrato in Fig.1.b (in basso).

La Figura 2, invece mostra il profilo di concentrazione dei cloruri predetta per tempi differenti. Anche in questo caso, la figura è riferita al Modello A (CP).

É evidente un buon accordo tra la predizione di modello e i dati sperimentali di Thomas e Bamforth. Nella stessa tabella sono anche indicati i valori dei parametri calibrati, per il Modello A e il Modello B. Al fine di confrontare quest’ultimi con gli altri approcci, sono riportati anche i valori degli stessi parametri riferiti ai risultati di Thomas and Bamforth.

Osservando i risultati sintetizzati nella Tabella 2, è possibile notare immediatamente che l’introduzione della dipendenza dal tempo della concentrazione dei cloruri sulla superficie C_s, come adottata nel Modello B, hanno effetti non trascurabili. Infatti, i risultati ottenuti dall’applicazione del Modello B al posto del Modello A, sembra differire molto rispetto ai dati indagati. Un’altra considerazione importante, concerne il fatto che, come la microstruttura del cemento diventa più sottile (come nel passaggio dalla miscela CP al CLA, con un livello crescente della quantità di ceneri volanti), il profilo dei cloruri tende ad essere indipendente dal tempo, come evidenziato in Fig. 4 (c). Inoltre, i risultati confermano che il processo di diffusione dei cloruri nel cemento con il tempo resta praticamente costante nei calcestruzzi porosi quando il fattore d’età tende a zero (m → 0).

Segue che l’uso di una relazione semplificata come l’Eq. (1) o (3) che non considera effetti a lungo termine, è legittimato nel caso di cementi porosi come il Portland (m → 0), perchè l’errore commesso è trascurabile. Al contrario, usando il modello con coefficiente di diffusione costante col tempo anche per cementi poco porosi (m → 1) (come per esempio il cemento di loppa d’altoforno), esso porta ad una stima inappropriata dei parametri, dovuta alla forte diminuzione del coefficiente di diffusione con l’età. Inoltre, i risultati confermano l’enorme variabilità di D_a e m. Si dovrebbe notare che con riferimento a Thomas e Bamforth nessuno valore del coefficiente di diffusione è riportato perchè può essere riferito ad uno specifico istante di tempo e perciò non può essere confrontato con altri valori che appaiono nella stessa tabella, essendo questi ultimi ottenuti dalla calibrazione in funzione del tempo. Invece, il confronto dei valori di m ottenuti con quelli di Thomas e Bamforth, mostrano che in nessun caso un valore maggiore dell’unità è ottenuto. Questo è dovuto al fatto che l’assunzione di m ≥ 1 non è analiticamente ammissibile. Perciò esiste un limite superiore per il valore di m. Questa è una delle differenze tra i coefficienti di diffusione medi considerati dal modello e quello istantaneo. Quando sono usati i coefficienti di diffusione istantanei questo limite non è presente. Non ci sono ragioni per i quali valori di m uguali a 1 o maggiori non siano adottati, come già osservato da Stanish e Thomas [22].

Per tutte le ragioni menzionate, i parametri ottenuti in questo lavoro con la procedura basata sugli algoritmi genetici prima descritti, sono determinati in maniera più rigorosa sia da un punto di vista analitico che concettuale e potrebbero essere usati per una stima più affidabile del tempo vita delle strutture in CA.

3. CONCLUSIONI

Sono state condotte analisi della dipendenza dal tempo degli elementi strutturali in CA soggetti a corrosioni localizzate indotte dai cloruri. Il lavoro sviluppa una procedura generale in cui i più raffinati modelli evolutivi che descrivono la penetrazione dei cloruri nel calcestruzzo sono selezionati e poi, una procedura calibrata basata sugli algoritmi genetici è usata al fine di incorporare la variabilità col tempo sulla stima dei parametri di taratura. L’approccio proposto è una tecnica molto affidabile perchè permette di superare le notevoli limitazioni concettuali che caratterizzano alcuni modelli evolutivi e aiuterebbe a migliorare l’accuratezza della predizione della vita di servizio.

4. BIBLIOGRAFIA

[1] C. A. Apostolopoulos, P. G. Koutsoukos, “Study of the corrosion of reinforcement in concrete elements used for the repair of monuments”, Construction and Building Materials (2007, article in press).
[2] P.S. Mangat, B.T. Molloy, “Prediction of long-term chloride concentration in concrete”, Mat. Struct. 27 338– 346, 1994.
[3] L. Mejlbro, “The complete solution to Fick’s second law of diffusion with time dependant diffusion coefficient and surface concentration. Proceeding of CEMENTA’s workshop on Durability of Concrete in Saline Environments”. Danderyd, Sweden, 1996.
[4] T. Luping, J. Gulikers, “On the mathematics of time-dependent apparent chloride diffusion coefficient in concrete”, Cement and Concrete Research 37, 589-595, 2007.
[5] C M. Collepardi, A. Marcialis, R. Turriziani, “Penetration of chloride ions into cement pastes and concrete”, J. Am. Ceram. Soc. 55 (10) 534–535, 1972.
[6] M. G. Stewart, D. Rosowsky, “Time-dependent reliability of deteriorating reinforced concrete bridge decks”, Structural Safety 20, 91-109, 1998.
[7] K. Takewaka, S. Mastumoto, “Quality and cover thickness of concrete based on the estimation of chloride penetration in marine environments”, in: V.M. Malhotra (Ed.), Proc. 2nd Int. Conf. Concr. Marine Envir., ACI SP-109, pp. 381–400, 1988.
[8] L. Tang, L.-O. Nilsson, Chloride Diffusivity in High Strength Concrete at Different Ages, Nordic Concr. Res., Publication, vol. 11, pp. 162–171, 1992.
[9] J. Crank, The Mathematics of Diffusion, 2nd ed. Clarendon Press, Bristol, 1975.
[10] M. Maage, S. Helland, J. Carlsen, Practical non-steady state chloride transport as a part of a model for predicting the initiation period, in: L.-O. Nilsson, J. Ollivier (Eds.), Chloride Penetration into Concrete, RILEM, pp. 398–406.
[11] Sandberg, P.: Critical evaluation of factors affecting chloride initiated reinforcement corrosion in concrete. Division of Building Materials, Lund Institute of Technology, Sweden. Report TVBM-7088, pp.24-25, 1995.
[12] L. Tang, Chloride Transport in Concrete — Measurement and prediction, PhD thesis, Publication P-96:6, Dept. of Building Materials, Chalmers Univ. of Tech., Gothenburg, Sweden, 1996.
[13] P.B. Bamforth, The derivation of input data for modelling chloride ingress from eight-year UK coastal exposure trials, Mag. Concr. Res. 51 (2) 87– 96, 1999.
[14] M.D.A. Thomas, P.B. Bamforth, Modelling chloride diffusion in concrete—effect of fly ash and slag, Cem. Concr. Compos. 29 487– 495, 1999.
[15] DuraCrete, Modelling of Degradation, EU-Project (Brite EuRam III) No.BE95-1347, Probabilistic Performance based Durability Design of Concrete Structures, Report, vol. 4–5, 1998.
[16] J. D. Cairns; D. Law; Prediction of the ultimate state of degradation of concrete structures. Proceeding of ILCDES 2003, Kuopio, pp169-174, 2003.
[17] K. Uji, Y. Matsuoka, T. Maruya, Formulation of an equation for surface chloride content due to permeation of chloride, Proceedings of 3nd Intl. Symp. Corrosion of Reinf. Concr. Constr. Elsevier, London, pp. 258–267, 1990.
[18] R.N. Swamy, H. Hamada, T. Fukute, S. Tanikawa, J.C. Laiw, Chloride penetration into concrete incorporating mineral admixtures or protected with surface coating material under chloride environments, Proc. of CONSEC, vol. 95, E & F N Spon, London, 1995.
[19] Choe D-F, et al. “Probabilistic capacity models and seismic fragility estimates for RC columns subject to corrosion”. Reliab. Eng Syst Safety doi:10.1016/j.ress.2006.12.015 (2007, article in press).
[20] J. Gulikers, Theoretical Backgrounds and Practical Applications of the Modified Error Function Solution for Modelling Time-dependent Chloride Ingress into Concrete, BSRAP-R-04012, Bouwdienst Rijkswaterstaat, Dec. 2004.
[21] L.-O. Nilsson, M. Carcasses, Models for Chloride Ingress into Concrete—A Critical Analysis, Report of Task 4.1 in EU-Project G6RD-CT-2002-00855, ChlorTest, 2004.
[22] K. Stanish, M.D.A. Thomas, The use of bulk diffusion tests to establish time-dependent concrete chloride diffusion coefficients, Cem. Concr. Res. 33 (1) 55–62, 2003.