www.edilweb.it - Da Galileo a Cauchy per elaborare la legge di Hooke

I grandi personaggi di questo articolo in ordine di apparizione:
G.Galilei (1564-1642)       Þ Concetto di carico (1638)
I.Newton (1642-1727)       Þ Azione e reazione (1669)
R.Hooke /1635-1702)       Þ “Ut tensio sic vis” (1679)
T. Young (1773-1829)       Þ Modulo di elasticità (1800)
A.Cauchy (1789-1857)     Þ Legge di Hooke. (1822)
C.L.Navier (1785-1836)   Þ E=modulo di Young (1826)

CONCETTO DI SFORZO

Galileo Galilei (1564-1642), oltre ad essere un grande filosofo e forse il massimo scienziato italiano, può rivendicare altri tre primati tra loro in stretta relazione per le ragioni che mi accingo a spiegare...

di Mario Collepardi Enco Journal anno IV n.16

Il primo è quello di essere stato il primo “pentito” della storia: pentito tra virgolette per indicare, cioè, che si era pentito solo per aver salva la vita quando, durante il papato di Urbano VIII, l’Inquisizione nel 1633 lo costrinse ad abiurare la sua tesi eliocentrica copernicana in favore di quella geocentrica tolemaica («Dialoghi dei Massimi Sistemi», 1630). Già nel 1600, d’altra parte, Giordano Bruno era stato condannato da Clemente VIII, e successivamente arso vivo, proprio per non aver chiaramente accettato di pentirsi dei suoi “errori”. Galileo, insomma, dopo aver a lungo tergiversato, capì che era il caso di pronunciarsi per un chiaro e pronto pentimento.

Il secondo primato di Galileo, conseguente al primo, è quello di essere stato il primo “pentito” condannato agli arresti domiciliari nella sua villa ad Arcetri presso Firenze.

Per evitare altri spiacevoli contraddittori con il Sant’Uffizio, Galileo durante gli arresti domiciliari che lo costrinsero ad Arcetri fino alla morte, seguitò sì a studiare occupandosi, però, di argomenti molto meno celesti e per lui meno pericolosi. Nel 1638 pubblicò la sua ultima grande opera intitolata «Discorsi e dimostrazioni matematiche intorno a due nuove scienze attinenti alla meccanica ed ai movimenti locali» (in appendice il frontespizio dell’opera). Ed è in questa opera, che Galileo forse non avrebbe mai portato a termine se non fosse stato condannato agli arresti domiciliari, che si può rintracciare il terzo primato che maggiormente in questa sede ci interessa: Galileo fu il primo ad occuparsi della resistenza meccanica in termini di rottura dei materiali sottoposti all’applicazione di un carico. Provò sperimentalmente, come era suo costume, che maggiore è la sezione di un certo materiale (di forma e geometria determinate: per esempio aste cilindriche), maggiore è il carico che occorre applicare alle due aste per provocare la rottura (Fig. 1).

Galileo forse intuì ma certamente non esplicitò il concetto di sforzo (s), inteso come forza per unità di superficie (Fig. 2), e si limitò ad esaminare solo il carico, cioè la forza F (Fig.2). Galileo non si accorse che dividendo il carico di rottura (100 Kg e 400 Kg rispettivamente nell’asta A e B di Fig. 1) per la sezione (S) ortogonale al carico (3.14 cm² e 12.56 cm² rispettivamente) si sarebbe ottenuto un unico valore:

100		400
-------	=	--------	=	31.85 kg/cm²
3.14		12.56

che rappresenta (così diremmo noi oggi) lo sforzo (s) capace di provocare la rottura del materiale nelle condizioni di prova sperimentate (provini cilindrici, applicazione dello sforzo a trazione, ecc.)

Dovettero passare quasi due secoli perché il concetto di sforzo fosse chiarito dal francese Augustin Cauchy. Ma di questo parleremo più avanti.

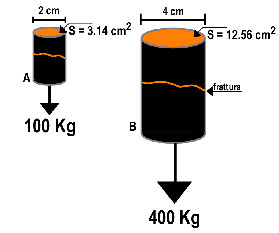
Fig.1 - Raddoppiando il diametro dell’asta cilindrica (da 2 a 4 cm) il peso che provoca la rottura aumenta di quattro volte (da 100 a 400 Kg).

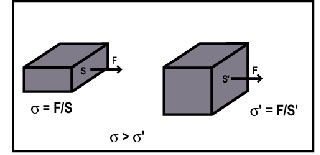
Fig. 2 - A parità di forza F applicata su due superfici diverse (Ss>s’) laddove la superficie è minore.

CONCETTO DI DEFORMAZIONE

Nella sua terza legge della dinamica, nota anche come principio di azione e reazione, il britannico Newton (1642-1727) afferma che quando esiste un’interazione tra due corpi la forza esercitata dal primo sul secondo è ad ogni istante eguale ed opposta alla forza esercitata dal secondo sul primo. Quasi in forma di omaggio al grandissimo Isac Newton, nel 1679 il britannico Robert Hooke (1635-1702) pubblicò un saggio intitolato «De potentia restitutiva or of a spring» a ulteriore conferma della terza legge di Newton, Hooke trovò che:

ogni solido si deforma (accorciandosi o allungandosi) quando è sollecitato e la deformazione si annulla se si rimuove la sollecitazione;
è proprio questa deformazione (tensio) che consente al solido di sviluppare l’azione opposta (vis) alla sollecitazione.

Fig. 3 - Reazione del gatto attraverso la deformazione dei tendini alla sollecitazione della bambina.

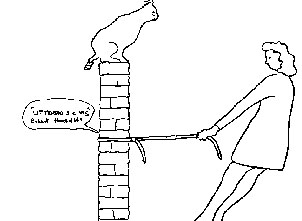
Fig. 4 - Reazione del muro (invisibile, ma c’è) alla sollecitazione della bambina.

Hooke sintetizzò le sue scoperte con il celebre aforisma «ut tensio, sic vis», (tanta la deformazione, tanta la forza). Il significato è il seguente: se tiro un elastico di gomma o la coda di un gatto (Fig. 3) ci si accorge visivamente della forza (vis) attraverso la deformazione reattiva (tensio*). Se invece la stessa sollecitazione è applicata ad un muro (Fig.4) la deformazione è meno o per niente visibile: eppure la deformazione esiste. La differenza tra la deformazione della coda del gatto e quella del muro sta nella diversa qualità (cioè elasticità) dei due materiali. Ma per cogliere questo significativo aspetto del problema si dovrà attendere Thomas Young, anch’egli britannico, più di un secolo dopo come si vedrà più avanti (vedi Tabella 1).

*tensio, dal latino tendere, originariamente significava "deformazione" nell'aforisma di Hooke; nel linguaggio ingegneristico attuale il termine "tensione" significa, invece, sforzo; la confusione semantica sembra propio trarre origine dal fatto che tensione (tensio) nel linguaggio di Hooke è "deformazione" reattiva che rappresenta lo sforzo (vis).

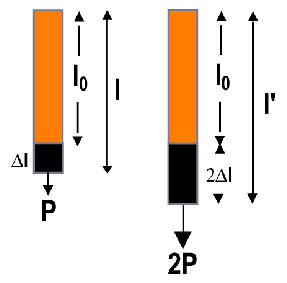
Fig. 5 - Applicando un carico P il filo si allunga di Dl = l – l₀; se si applica un carico doppio (2P) anche l’allungamento raddoppia l' – l₀ = 2 Dl. Hooke colse bene questo aspetto.

Per completare l’esame del lavoro di Hooke occorre evidenziare il limiti della sua indagine, simili a quelli riscontrati nell’indagine di Galileo. Hooke si accorge che se due molle o due fili, entrambi di lunghezza l₀, sono tirati l’uno con un peso (2P) doppio dell’altro (P), anche l’allungamento è l’uno il doppio dell’altro (Fig. 5). Sfuggì, però ad Hooke che l’allungamento significativo non è quello assoluto (l – l₀ = D l), ma piuttosto quello relativo alla lunghezza iniziale (l₀)

		l-l₀		D l
e	=	--------	=	---------
		l₀		l₀

L’importanza della deformazione unitaria (e) apparirà più evidente se si applica lo stesso carico (P) a due provini dello stesso materiale con lunghezza originale diversa: l₀ e 2l₀ (Fig. 6). L’allungamento assoluto è diverso (maggiore nel provino più lungo) ma l’allungamento relativo (e) è lo stesso (a parità di sforzo e di materiale) indipendentemente dalla lunghezza originale (l₀ oppure l’= 2l₀).

Nonostante questi limiti, il contributo di Hooke alla teoria dell’elasticità rimane di enorme importanza nel campo dell’ingegneria al punto che alla legge sull’elasticità verrà poi legato il suo nome (legge di Hooke). Tuttavia Newton, che sopravvisse ad Hooke di 25 anni, trascorse il resto della sua vita a denigrare il lavoro di Hooke per futili ragioni di carattere personale alle quali non sfuggono neppure i grandissimi uomini (leggere in Appendice “Quel buontempone di Hooke”).

Dato il grande prestigio di Newton, la sua denigrazione nei confronti di Hooke e del suo lavoro sull’elasticità provocò, purtroppo, discredito presso gli scienziati ed i tecnici del Settecento nei confronti del lavoro di Hooke con grave nocumento per l’immediato progresso della teoria dell’elasticità.

TEORIA DELL'ELASTICITA'

In una relazione presentata all’Accademia delle Scienze Francesi nel 1822, il giovane matematico Augustin Cauchy (1789-1857) dimostrò che la deformazione, quella relativa (e) e non quella assoluta (D l) misurata da Hooke, era funzione (molto semplice) dello sforzo s = F/S e non della forza (F) (Fig. 2).

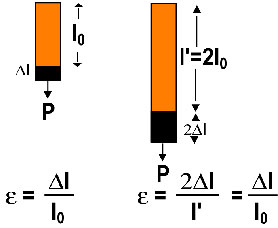
Fig. 6 - Applicando lo stesso carico P l’allungamento assoluto è maggiore nel provino più lungo (l’) ma l’allungamento relativo e è lo stesso. Hooke non se ne accorse.

Cauchy (nominato barone dal governo francese proprio per i suoi studi sulla teoria dell’elasticità) indicò anche che lo sforzo s è concettualmente, oltre che dimensionalmente, analogo alla pressione. Come all’interno della gomma di una ruota automobilistica gonfiata alla pressione di 2 Kg/cm² tutto il gas in ogni punto è sottoposta alla pressione di 2 Kg/cm², così pure all’interno di un solido sollecitato a compressione tutti gli atomi (o ioni, o molecole) debbono essere immaginati come se fossero sottoposti alla stessa sollecitazione con deformazione delle reciproche distanze interatomiche.

In sostanza tutti i legami tra gli atomi del materiale si deformano al pari del materiale stesso visto esternamente (Fig. 7). Da un punto di vista pratico è più facile misurare la deformazione del materiale visto esternamente a seguito di una sollecitazione a compressione, s_c, o a trazione, s _t (Fig. 8), che non la variazione della distanza interatomica.

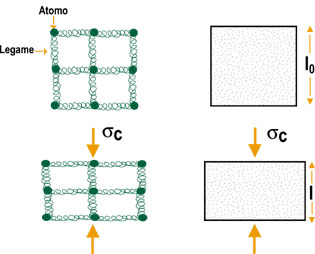
Fig. 7 - L’applicazione di uno sforzo a compressione (s_c) schiaccia il solido (a destra) e deforma similmente tutte le distanze tra gli atomi.

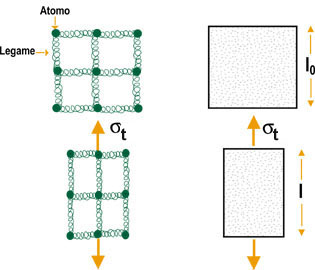
Fig. 8 - L’applicazione di uno sforzo a trazione (s_t) allunga il solido (a destra) e deforma similmente tutte le distanze tra gli atomi.

Tabella 1 - Modulo elastico (E) di alcuni materiali da costruzione (vedere l’Appendice per le unità di misura).

Materiale	E (GPa)
Diamante	1000
Carburo di Silicio	450
Nichel	215
Acciai	195-215
Titanio	85-130
Alluminio	70-80
Calcestruzzo	20-40
Materie plastiche	0.1-5
Gomma	0.001-0.01

Per quanto paradossale possa apparire, la mancata distinzione, da parte di Hooke, tra deformazione assoluta D l = l – l₀ e deformazione unitaria e = D l/l₀ bloccò per molto, fino ai tempi di Cauchy, la diffusione della “legge di Hooke” nella forma semplice oggi a noi nota:

s = Ee

dove E è la costante di proporzionalità tra sforzo e deformazione unitaria.

Thomas Young (1773-1829) fu il primo a capire l’importanza del fatto che E varia con il materiale (Tabella 1). E oggi si chiama modulo di elasticità o modulo di Young in suo onore su proposta fatta nel 1826 dal francese Claude Louis Navier (1785-1836) tre anni prima che Young morisse (in Appendice il riquadro “Quel pasticcione di Young”).

Se si confrontano due tipici materiali da costruzione come l’acciaio (molto rigido) ed il calcestruzzo (più deformabile) si può osservare (Tabella 1) che il primo presenta un valore di E di circa 20 GPa, cioè 7 volte circa maggiore del valore di E per il calcestruzzo (circa 30 MPa). Quale è il significato di questa differenza nel valore di E? Il significato è il seguente: per realizzare la stessa deformazione e nei due materiali occorre applicare uno sforzo (s ), sull’acciaio che è circa 7 volte maggiore dello sforzo applicato sul calcestruzzo.

DEFORMAZIONE DELLA STRUTTURA E DEL PROVINO

Le ragioni che non permisero ad Hooke di cogliere l’importanza della deformazione unitaria (e) rispetto a quella della deformazione assoluta (D l) risiedono nella difficoltà di misurare le deformazioni unitarie su strutture reali per lo più di forma solitamente complessa ed in presenza di sollecitazio ne anch’esse complesse.

Per studiare il comportamento dei diversi materiali da costruzione a seguito di sollecitazioni applicate, occorrono tre condizioni:

sottoporre ad indagine una porzione ben definita di materiale “omogeneo” (mattone, acciaio, calcestruzzo, ecc.);
la porzione ben definita di materiale “omogeneo” si deve presentare in forma di una geometria relativamente semplice (prisma, cilindro, cubo, ecc.) che prende il nome di provino;
la sollecitazione applicata deve essere di tipo semplice, solitamente monoassiale (compressione o trazione) o comunque facilmente maneggiabile matematicamente (taglio, flessione).

Nella Fig. 9 sono mostrati tre tipici provini (prismatico per il mattone, cilindrico per l’acciaio, cubico per il calcestruzzo) sottoposti a sollecitazione rispettivamente di flessione (s_f), di trazione (s_t) e di compressione (s_c).

Stabilite le dimensioni del provino si potrà misurare più facilmente le sezioni trasversali agli sforzi e le deformazioni assolute. Si potrà quindi trasformare un carico P in uno sforzo una volta noto il regime tensionale nella sezione s (=P/S) ed una deformazione assoluta (D l) in una deformazione unitaria (D l/l₀).

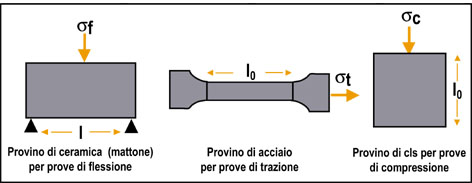
Fig. 9 - Provini e tipi di sforzo per caratterizzare il comportamento dei materiali.

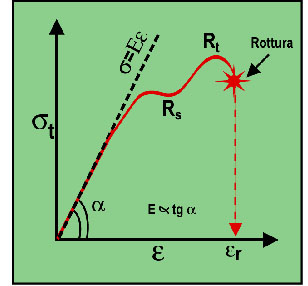
Fig. 10 - Curva sforzo-deformazione (s-e)

Applicando, attraverso le macchine, carichi semplici (per esempio di trazione) e noti, e misurando (mediante estensimetri) le variazioni dimensionali, si potrà ricostruire un diagramma “sforzo-deformazione”. Nel grafico della Fig. 10 si trovano alcuni dati interessanti che approfondiremo nelle prossime lezioni: il massimo sforzo che è in grado di sopportare il materiale (R_t, resistenza meccanica); la resistenza allo snervamento (R_s) che indica lo sforzo nella curva s - e che corrisponde solitamente ad un piccolo “pianerottolo” nella deformazione; il massimo allungamento (e_r) che subisce il materiale al momento della rottura (materiali fragili e duttili presentano e_r rispettivamente piccoli o grandi); la pendenza della curva in particolare nel tratto iniziale dove tra s ed e esiste proporzionalità lineare (cioè vale la legge di Hooke: s=Ee); l'area sottesa dalla curva s-e che è proporzionale al lavoro speso per rompere il materiale (tenacità). In particolare, il valore di E (cioè la pendenza della curva nel tratto lineare) rappresenta la rigidità specifica del materiale e cambia da materiale a materiale (Tabella 1).

Approfondimento: Per un approfondimento dell’argomento sulla teoria dell’elasticità si consultino i libri “Structures or Why Things Don’t Fall Down” e “The New Science of Strong Materials or Why You Don’t Fall through the Floor” di J:E: Gordon, Penguin Books, London, 1991, (disponibili anche in italiano nella collana Biblioteca EST, Mondadori). Da questi libri sono stati desunte gran parte delle informazioni riportate qui.

APPENDICE

Quel pasticcione di Young

A dire il vero Young era geniale ma un po’ pasticcione nell’esposizione. Così illustrò nel 1800 all’Ammiragliato Britannico (che doveva finanziare i suoi studi) il concetto di modulo elastico:

“Il modulo di elasticità di qualsiasi sostanza è una colonna della medesima sostanza, capace di esercitare sulla propria base una pressione che sta al peso che provoca un certo grado di compressione come la lunghezza della sostanza sta alla diminuizione della sua lunghezza”

E l’Ammiragliato giustamente rispose: “Benché la scienza sia molto rispettata ed il vostro saggio sia molto stimato, esso è troppo erudito, ..... in breve non lo si è capito”.

Forse anche per questo Young dopo aver insegnato la teoria dell’elasticità alla Royal Institution di Londra (dove era professore di filosofia naturale) lasciò la cattedra e tornò a fare il medico.

Quel buontempone di Hooke

Robert Hooke fisico e naturalista con grandi capacità di sviluppare applicazioni pratiche. Inventò orologi, microscopi, molle, giunti meccanici e diaframma ad iride per macchine fotografiche.

Nella vita privata era un godereccio amante della vita. Ad Hooke piacevano molto le donne: tutte, o quasi, inclusa sua nipote Grace.

Per contro Isac Newton, grandissimo scienziato teorico, era un matematico e fisico. Nel privato Newton era un po’ snob (come accade anche oggi a qualche “professorone”), studioso di teologia, poco incline alla “carne”. Ce n’era abbastanza perché odiasse quel buontempone di Hooke.

Modulo di Poisson

Quando è sottoposto a compressione, il materiale si accorcia verticalmente (e_v) lungo l'asse dello sforzo e si dilata lateralmente (e_l) nella direzione ortogonale (Fig. 7): il rapporto e_l/e_vsi chiama modulo di Poisson (n). Anche nella trazione (Fig. 8) il modulo vale e_l/e_v.